Continuous Variable

A continuous variable can in theory take any value over its range, as opposed to a discrete variable.

• The real world is discrete: in practice data for continuous variables are generally rounded to some level of measurement accuracy.

Features of Continuous Variables

• Asymmetry
  • the distribution may not be symmetric like Normal Distribution
  • the distribution may be skewed to the left or right
    • A distribution is called skewed left/negative if, as in the distribution graph, the left tail (smaller values) is much longer than the right tail (larger values)
    • A distribution is called skewed right/positive if, as in the distribution graph, the right tail (larger values) is much longer than the left tail (smaller values)
    • 
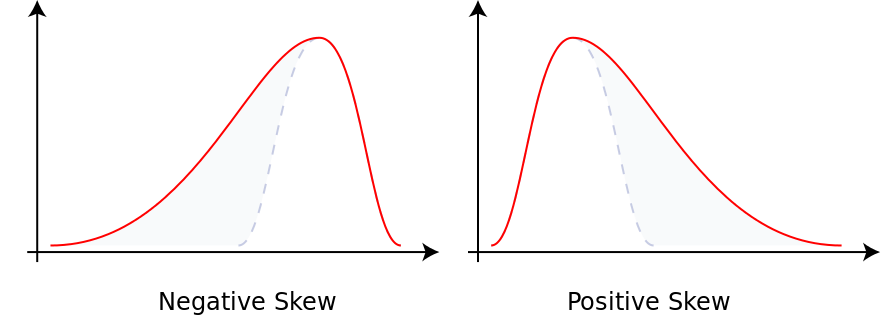
  • distributions of income
• Outliers
  • there may be data far from the rest of the data
• Multimodality
  • the distribution may have more than one peak
  • the mode is the value that appears most often in a set of data values
    • For a discrete Random Variable, the mode is ${\text{argmax}}_{k}P(X=k)$
    • For a continuous Random Variable, the mode is the local maxima of the PDF
• Gaps
  • There may be ranges of values within the data where no cases are recorded
• Heaping
  • some values may occur unexpectedly often
• Rounding
  • Only certain round values (like integers) are found
• Errors/Impossibilities

Different graphs emphasize different features.

Graphs

• Histogram
  • asymmetry
  • multimodality
  • gaps
  • heaping
  • rounding
• Boxplot
  • outliers
  • statistics
  • ❌ multimodality
• Density Curve
  • distribution
  • asymmetry
  • multimodality
  • ❌ gaps
  • ❌ heaping
• Ridgeline
• Bar Chart
  • gaps, heaping
  • treating discrete values as Categorical Data
• Cleveland Dot Plot
  • gaps
  • [-] heaping
• Q-Q Plot
  • distribution
  • asymmetry
  • multimodality

Combine Continuous Variables and Categorical Variables

by zcysxy